Compatibility
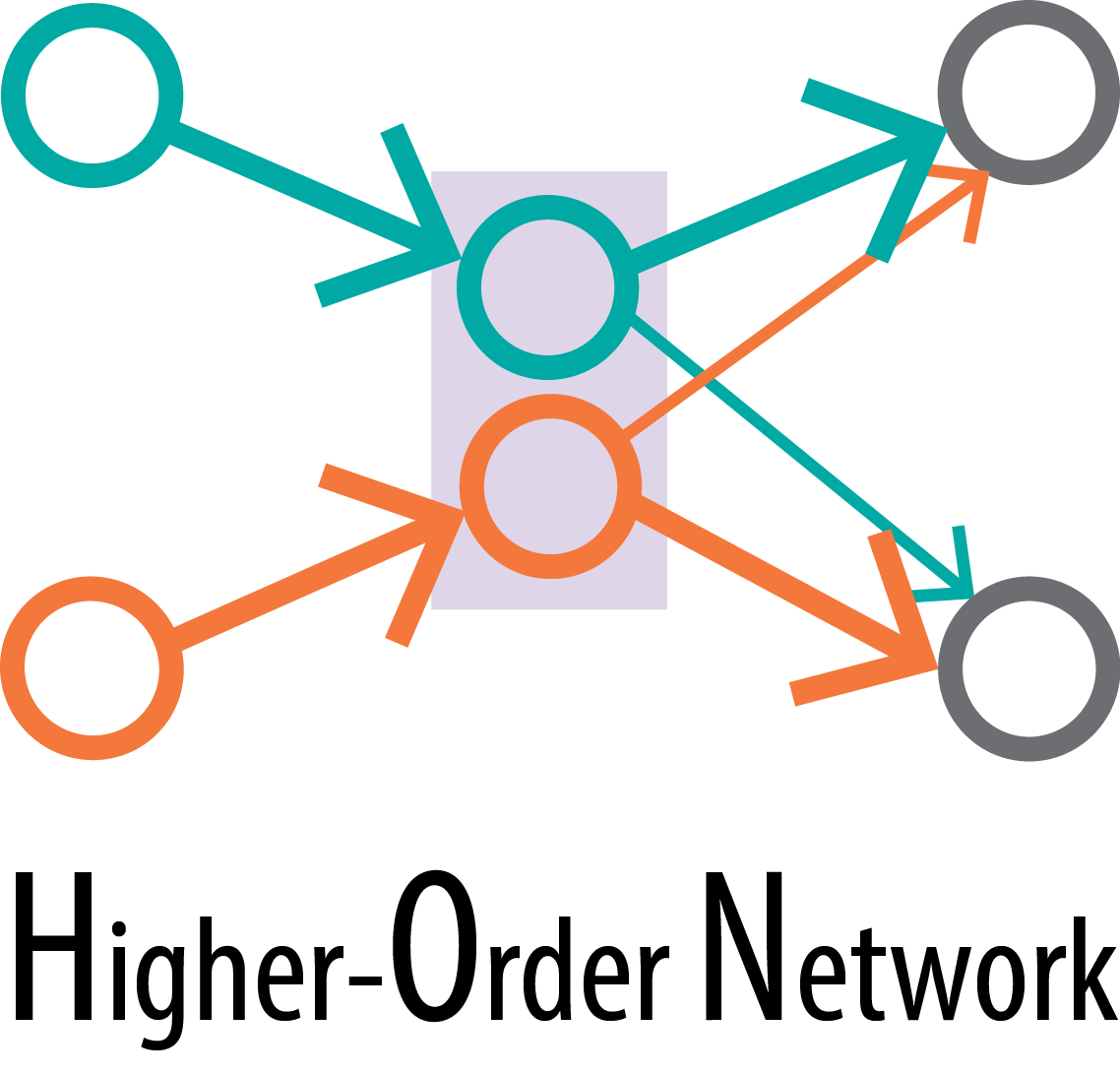
For a ship at Singapore, given the network structure, where the ship will go next is proportional to the edge weights. This shows a Markovian property of the first-order network representation.
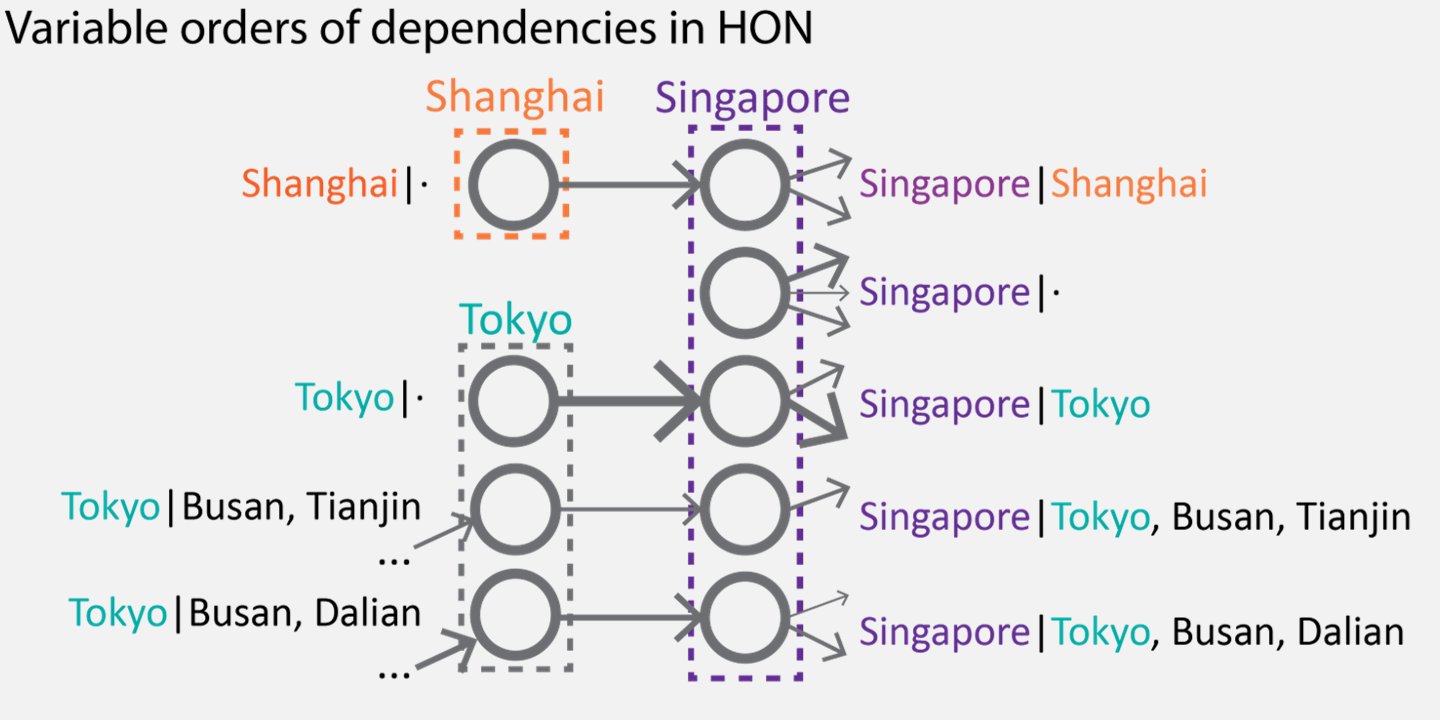
In HON, we break down Singapore into two nodes, Singapore given Tokyo and Singapore given Shanghai. These two nodes have their respective edge weights to LA and Seattle. While ships still perform random walks, coming from different paths to Singapore will now have different probabilities to choose the next step.
Everything in the formula is unchanged except the labeling of nodes, which means that this higher-order network keeps the data structure consistent with first-order network, and is directly compatible with existing tools.
Variable orders means scalability
What if the movement on the network depends on more than two steps, say, five steps ago? One potential approach is to break down every node five times to embed more information, creating a fifth-order network. While the fixed-order network is easy to build, it does not scale well. By forcibly breaking down every node into a certain high order will make the network exponentially more complex, considering how many potential combinations of five previous steps can be.
Instead, we propose to use a variable-order representation, that uses the first order when it is sufficient, and uses higher orders only when necessary. As a result, we can represent variable orders of dependencies in the same network. The best of all, the network size is magnitudes smaller than fixed-order networks, making it scalable for big data.
Challenge #1: how do we decide the order for each node & edge?
Challenge #2: how to connect nodes with variable orders in a network?
Workflow
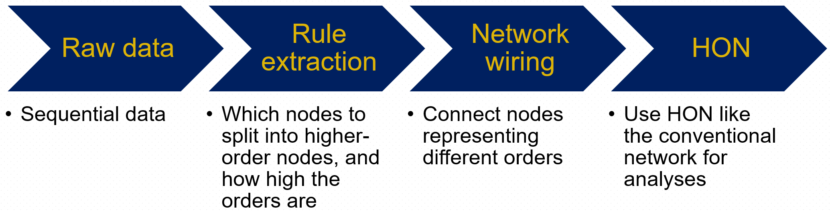
Rule extraction
The rule extraction process works as follows. In the shipping example, from the raw shipping trajectories,
- Count how many ships are going from Singapore to the next port;
- Normalize the distributions;
- Given one more previous step, say Shanghai, see how that changes the distribution of the next step from Singapore; if the change is significant, then there is second order dependency here. This process is then repeated recursively for higher-orders.
Network wiring
After deciding the orders of dependencies, we
- First construct a first-order network in the conventional way;
- Then for every second order rule, add the corresponding node;
- Rewire the previous first-order link to connect to the new higher-order node; then repeat the process for third order rules and so on.
- Finally, for the highest order nodes, rewire their out-edges to connect to nodes with the highest orders possible.
Scalability
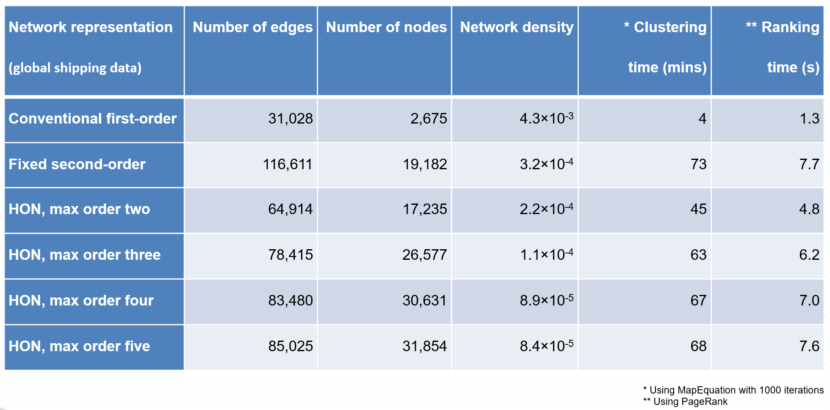

HON+: a fundamentally improved HON construction algorithm
Latest update: the HON construction algorithm is now
- Parameter-free
- Scales up to arbitrarily high order of dependencies
- Magnitudes faster and memory friendly
- Python code available on GitHub
- Paper available on arXiv